Greetings and salutations my old friend! I pen this epistle to you from my post at the Borgesian Archives of Moral Science here at Cassius University, having now just noticed your public request for advisement. I would be immersed in solitude at the moment if it wasn’t for our mutual comrade Reverend Kishkumen; I had ordered a high quality facsimile Codex Bezae and it came in today and the good Reverend couldn’t resist getting the first crack at it ahead of the esteemed Professor Symmachus while also imbibing more than a few cans of White Claw that I had stashed away in a hidden refrigerator.
There can be no doubt that philology is thirsty work and with these allegations of Aramaisms in this particular manuscript, the Reverend is taking an especially close look at Acts 13:29. See for yourself:

I imagine you can see it straight away; we have “taking down” followed with an “and” as if there was a finite verb instead of the participle. This is permissible in Aramaic of course, a participle followed by an “and” which, in turn, a finite verb can be introduced. Possible Aramaism?
Glancing at the Latin portion of the manuscript the Reverend noticed something interesting:

Can you see it? It took me a minute, but it became clear as day: “deposuerunt et posuerunt in monumento”. Two finite verbs linked by an “and”! It seems the rumors of a supposed Aramaism in this manuscript is nothing more than a simple scribal error.
I really should put a halt to this aside about classical languages, you were not seeking insight into comparative linguistics. Here at Cassius, we’ve taken inspiration from the ancient Chinese and Indian sages who insisted one must first become a competent grammarian before philosophizing in earnest. A sentiment I’m sure you agree with.
So on to the business at hand:
Before getting into particulars, I would recommend you obtain a copy of Laurence Jonathan Cohen’s monograph ‘The Probable and The Provable’ for background reading. There is quite a mountain of literature out there about how to use probability theory to model the convergence of evidence and Cohen is at the heart of it (along with Charles Sanders Pierce, but Cohen is much more accessible at this juncture).Daniel C. Peterson wrote:I’m interested in feedback on the reasoning that is set forth above. Not so much about reader opinions regarding near-death experiences in and of themselves but on the subject of whether the methodology of assessing levels of persuasion is substantially sound. Please advise.
Now I’ve carefully read your blogpost (I am, afterall, a student of yours as much as I am of anyone else) and gathered that you have intuited agreement from multiple reports can establish a high probability for what is agreed upon by those reports. Taken individually those reports might have poor evidentiary value, yet taken as a whole, those same reports can provide an evidentiary value greater than their mere sum. Is this correct?
If the above is correct then it is a tricky business, but I can offer you some assistance in putting this notion to a preliminary test that should serve as a good starting point for further research. Michael Huemer put out a simple model of how agreement could work in his 1997 paper ‘Probability and Coherence Justification’ that utilizes the kind of probability calculus amenable to your apologetic endeavors.
Thankfully you have invoked the use of Bayes theorem in years past and with your familiarity with it, we can simply dive into it. Let us suppose the following:
H = There is a heavenly afterlife.
~H = There is not a heavenly afterlife.
E₁ = Hugh Nibley reports that he has experienced an afterlife through a NDE.
E₂ = Sterling McMurrin reports that he has experienced an afterlife through a NDE.
Now to formalize it:
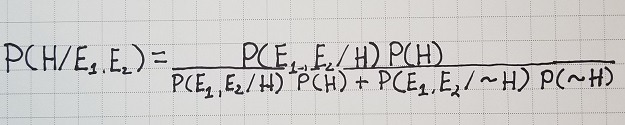
More work needs to be done because we need to make two assumptions about the independence of the witnesses. We must assume that the reports of both Nibley and McMurrin are independent conditional on the truth and the falsity of H: P(E₂/E₁, H) = P(E₂/H) and P(E₂/E₁, ~H) = P (E₂/~H). From this we effortlessly glean: P(E₁,E₂/H) = P(E₁/H) P(E₂/H) and also P(E₁,E₂/~H) = P(E₁/~H) P(E₂/~H).
We must also suppose that Nibley and McMurrin have equal credibility as individuals. Let us state that that i denotes their initial credibility: i = P(E₁/H) = P(E₂/H). Naturally it follows that: P(E₁,E₂/H) = P(E₁/H) P(E₂/H) = i².
Lastly it is given that if either Nibley or McMurrin give a testimony that is ultimately false, any of the n - 1 alternative explanations for an NDE can be invoked with equal probability. So the probability that either Hibley or McMurrin testifies falsely as to the nature of their NDE can be represented as P(E₁/~H) = P(E₂/~H) = (1 - i)/(n-1).
Considering what we stated above regarding independent conditionals and the falsity of the hypothesis, we find that: P(E₁,E₂/~H) = P(E₁/~H) P(E₂/~H) = (1-i)²/(n-1)². Combining this all into a neatly packaged model we get:
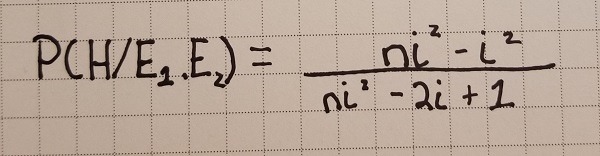
With all of that in order, let us get to proving the concept. The jointly posterior probabilities are influenced by two factors: the number of equally likely explanations for an experienced NDE and the individual credibility of each testimony. If there are ten explanations (equal in likelihood) for experienced NDEs (n=10) and if a heavenly afterlife is one of them, then P(H) = .1. Continuing on, let us assume that i=P(E₁/H)=P(E₂/H)=.5. Feeding that into the above model returns P(H/E₁,E₂) = .9.
So if neither Nibley nor McMurrin’s testimony is good enough alone to render a high enough value to make a heavenly afterlife probable, combining them renders the value high enough to be considered highly probable. Thus, we have a simple model that demonstrates a convergence of evidence that your intuition was driving you towards.
Alas, there are a few flies in the ointment.

If you ever do decide to study Cohen, I’d draw your attention to pages 100 to 107 where his infamous corroboration theorem is taken up. Testimonial independence is a sensitive matter and as he demonstrates, witnesses familiar with each other and each other’s testimonies will compromise the needed independence. Thus, if all the witnesses to the gold plates are, at least, one time compatriots of Joseph Smith, or the testimonies of NDEs are drawn from a pool of people who actively participate in communities that discuss NDEs, such testimonial independence can be seriously questioned.
Secondly, Huemer’s contribution shows that the model under consideration has an interesting implication. No convergence takes place if the individual testimonies themselves are irrelevant or somehow rendered useless: i = P(H) = 1/n. Plug that into the equation returns P(H/E₁,E₂) = 1/n = P(H) and we now have a demonstration that combining testimonies doesn’t move the posterior probability up. The takeaway being that full agreement does not necessarily result in having an effect on the likelihood of obtaining the truth of a supposed event, only if the circumstances are just right.
Speaking of circumstances, they dictate that I end my missive on that note Daniel, if you require any further assistance in the matter, please don’t hesitate to reach out. The full resources of Cassius University are at your disposal, should you but ask.
Yours,
Alfonsy Stakhanovite.
